여기부터는 상태방정식의 모델이 적용되지 않는 혼합물의 활동도계수를 추정하는 방법에 대해 다루어볼 것이다.  일반적으로 이러한 추정에서는 혼합물에 대하여 다음과 같이 구별하는 것이 유용하다.

• 단순 액체 혼합물  :  순수한 유체를 혼합하여 같은 온도와 압력의 혼합물을 형성하는 경우
• 복잡한 액체 혼합물  :  순수한 성분들을 혼합하여 같은 온도와 압력의 혼합물을 형성하되, 최소한 한 성분은 혼합물 형성 전의 상태가 액체상태가 아닌 경우

   여기서는 단순 액체혼합물의 경우를 살펴볼 것이다.  이 경우, 혼합에 따른 Gibbs 자유에너지의 변화는 다음과 같다.

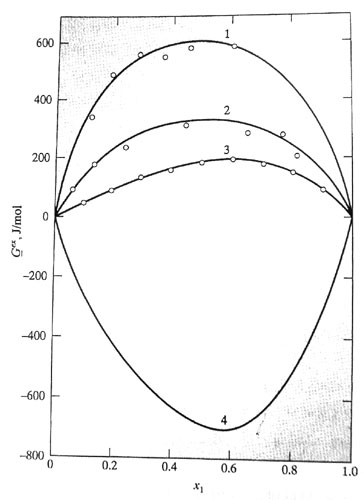
대표적인 예로 벤젠-2,2,4-트리멜린 펜탄계의 과잉혼합 Gibbs 자유에너지를 다음 그림에 표현하였다.  이 그림의 곡선들은 단순한 형태를 가지고 있다.  따라서 혼합의 과잉 Gibbs 자유에너지를 예측하는 한 가지 방법은 조성의 다항식으로 표현하는 것이다.  제한된 양의 실험데이터를 사용하여 적절한 다항식의 매개변수들을 결정하고, 모든 조성 범위에 걸친 과잉 Gibbs 자유에너지와 액상의 활동도 계수를 추정하는 것이다.  물론, 과잉 Gibbs 자유에너지를 나타내기 위하여 선택된 임의의 수식은 Gibbs-Duhem식을 만족해야 하며, 그림의 데이터처럼 x₁→0 또는 x₁→1일 때 0이 되어야 한다.

   이러한 조건을 만족시키는 가장 단순한 형태는 다음과 같다.

   활동도 계수의 정의를 적용시키면 다음의 결과를 얻게 되며, 이 결과를 1-상수 Margules 모델이라고 부른다.

   1-상수 Margules 모델은 비슷한 크기와 형태 그리고 화학적 특성을 가진 성분들로 이루어진 혼합물에 대해서만 활동도계수의 거동을 잘 나타낸다.  그러나 좀 더 복잡한  계에 대해서는 타당하지 못하다.  특히 일반적인 혼합물의 과잉 Gibbs 자유에너지는 몰분율의 대칭함수가 되기 힘들다.  이러한 경우 식(2)를 확장해야 하는 필요를 가지느데, 그 일반화 중 하나는 다음과 같으며, 이를 Redlich-Kister 다항식이라고 부른다.

   식(4)에서 A≠0, B≠0, C=D=…=0 이면 다음의  결과를 얻는다.

여기서

이 결과를 2-상수 Margules 모델이라고 부른다.

|  복영근(Pock. young-keun)  |  www.peaceone.net  |  dreamer@peaceone.net  |

<< 아름다운 문화를 만들어 갑시다 ... ^^ >>