
지금부터는 당분간 어려운 주제를 미루기 위하여 Close system에 한정하여 설명할 것입니다. Open system에 관한 내용은 몇 가지의 사항을 추가로 포함하여 살펴보아야 하므로 후에 다루기로 하겠습니다. Close system에서는 물질의 양이 변하지 않으므로 시스템의 물질이 이떻게 구성되어 있는가에 대해서는 고려할 필요가 없게 됩니다.
|
1. 열 출입에 의한 시스템의 에너지 변화 : ΔE = Q |

|
2. 일(work)에 의한 시스템의 에너지 변화 : ΔE = -W |
이러한 일의 형태는 역학적, 전자기적, 중력 등 매우 많은 종류가 있습니다. 이 중 대부분 다루어지는 형태는 외부 힘이나 압력에 대응하는 역학적 일이며, 다른 형태의 일도 비슷한 수학적 표현으로 대치할 수 있습니다.
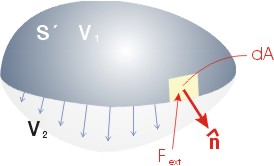
이 그림은 시스템 S'가 외부의 힘을 받아 부피가 V1에서 V2로 변화되는 것을 표현한 모형입니다. 이 과정을 수학적으로 표현하기 위하여 미소 표면적 dA에서 받은 힘에 대한 시스템의 대응일을 살펴보도록 하겠습니다. 미소 일은 외부 힘에 대하여 움직인 미소 거리를 곱한 값이 되므로 다음과 같이 쓸 수 있습니다.
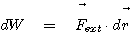
V1이 V2로 변할 때 시스템에 의해 한 일은 이 식을 전체 변화에 대해서 적분하면 구할 수 있게 됩니다.
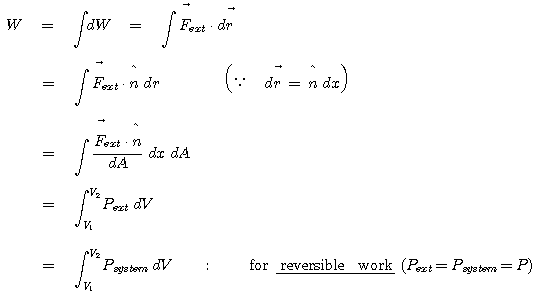
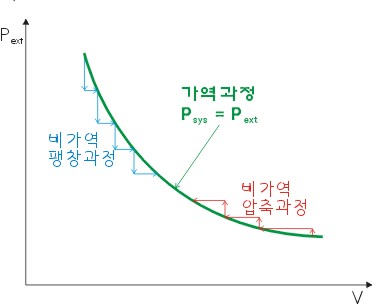
여기서 한가지 기억해야 할 사항은 가역과정(reversible process)에서만 등호가 성립한다는 점입니다. 우리가 경험하는 대부분의 실 세계는 거의 비가역 과정이므로 등호가 성립하는 경우는 매우 특별한 경우 외에는 존재하지 않습니다. 비가역과정(irreversible process)에서는 일에 의하여 시스템의 부피가 팽창하는 경우 가역과정에서 얻은 일의 양보다 적은 양의 일을 하게 됩니다. 왜냐하면 행해진 일이 전부 부피를 팽창하는 데 사용되는 것이 아니라 외부 마찰이나 진동 및 소음 등 다른 형태의 에너지로 소모되기 때문입니다. 이 과정을 간단히 요약해 보면 다음과 같이 표현해 볼 수 있습니다.
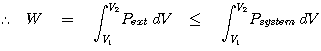
이 때 등호는 가역과정을 의미합니다.
|
3. 시스템의 총 에너지 변화 : ΔE = Q - W |
Closed system에서 상태변화에 대한 총 에너지변화를 생각해 보도록 하겠습니다. 상태 A에서 다른 상태 B로 진행되는 과정에서 변화하는 총 에너지의 양은 다음과 같이 표현할 수 있습니다.

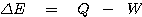
이 식은 바로 과정 속에서 변화되는 총 에너지의 양을 나타냅니다. 이 식을 총 변화에 대한 적분의 표현으로 다음과 같이 표현할 수도 있습니다.
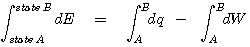
왼쪽의 총 에너지의 항은 실험적으로 경로에 무관함이 알려져 있습니다. 즉 총에너지는 상태함수이며 따라서 dE는 완전미분방정식의 조건을 만족합니다. 한편 오른쪽의 열량과 일의 항은 앞에서도 살펴보았듯이 각각 경로에 의존하는 함수이며 완전미분의 조건을 만족하지 않습니다. 그러나 이들 두 항의 조합은 언제나 총 에너지의 변화와 일치하게 됨을 알 수 있습니다.
따라서 시스템 상태의 모든 변화에 대한 정보를 다음과 같이 요약하여 표현할 수 있습니다.
|
|
이 결과식은 바로 열역학 제 1법칙(the First Law of Thermodynamic)을 나타내며, 에너지 보존법칙으로 잘 알려진 사항입니다.
여기서 일(work)은 외부 압력에 대응하는 에너지로 주로 나타나게 되며, 이 과정은 다음과 같이 쓸 수 있습니다.
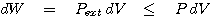
물론 여기서 등호는 가역과정에서만 성립합니다. 설명의 편의를 위해서 가역과정을 가정하면 열역학 제 1법칙은 다음과 같이 표현됩니다.
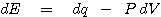
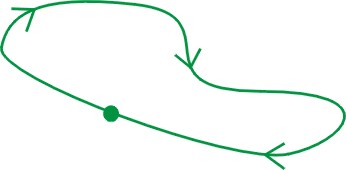
특히 경로가 닫힌 경우는 cyclic path라고 하며, 이 때의 에너지 변화를 살펴보도록 하겠습니다.
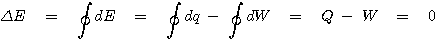
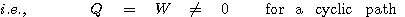
가역과정에서 Cyclic path의 경우에는 에너지의 변화가 "0"이며, 즉 에너지는 보존되고 따라서 열량 Q와 일 W는 같은 값을 가지게 됩니다. 열량 Q와 일 W는 단지 에너지의 두가지 다른 형태이고 그 각각은 보존되지 않으나 그들의 합인 총 에너지는 항상 보존됩니다. 일반적으로 열량의 단위인 [cal]와 일의 단위인 [J]의 관계를 알아두는 것은 매우 유용합니다.
Note : 1 cal = 4.184 J
|
4. 내부 에너지 (internal energy : U) |
열역학 제 1법칙의 관점에서 볼 때 에너지의 절대적 값은 큰 의미를 갖지 않습니다. 그 보다는 에너지 변화에 대한 차이값이 실재적인 물리적 의미를 가지며, 실험에 의해서 측정되는 값도 바로 이 값입니다. 따라서 어떤 임의의 기준 상태에 있는 시스템의 에너지를 "0"으로 가정하고, 어떤 다른 상태에 있는 시스템의 상대적 에너지를 사용하는 것이 매우 편리합니다. 바로 이 상대적 에너지의 값을 내부에너지(internal energy)라고 부르며, U로 표기하는 것이 일반화 되어 있습니다.
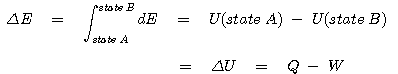
이러한 이유로 에너지의 상대적 의미를 인정한다는 조건으로 내부에너지는 총 에너지를 대체하는 경우가 많습니다. 따라서 가역과정에서 다음과 같이 사용하는 것이 가능합니다.
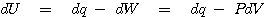
|
5. 일정 부피에서의 열역학 제 1법칙 |
열역학적 시스템의 부피(V)가 고정된 상태에서 상태(state)가 변할 때를 조사해 보도록 하겠습니다.
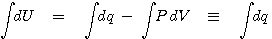
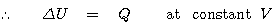
즉, 일정 부피에서 시스템의 내부에너지 U의 변화는 출입한 열량과 같습니다.
|
6. 일정 압력에서의 열역학 제 1법칙과 엔탈피(enthalpy) |
다음으로 열역학적 시스템의 압력(P)가 고정된 상태에서 상태(state)가 변할 때를 조사해 보도록 하겠습니다.
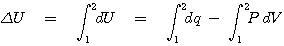
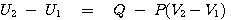
|
|
|
(1) |
식(1)에서 다음의 새로운 상태량(H)을 정의하면 매우 편리한 해석적 도구로 활용할 수 있습니다.

이렇게 정의된 상태량 H를 엔탈피(enthalpy)라고 하며, 경로에 의존하지 않는 상태함수입니다. 엔탈피를 사용하여 식(1)을 다시 쓰면 다음과 같습니다.
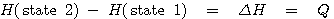

즉, 시스템의 압력이 일정한 상태에서 시스템에 출입한 열량은 그 시스템의 엔탈피 변화와 같습니다. 따라서 일정 압력하에서(특히 대기압 하에서) 어떤 시스템의 반응열(heat of reaction)과 융합열(heat of fusion)은 각각 반응 엔탈피와 융합 엔탈피와 동일한 의미로 사용됩니다. 일반적으로 열역학적 작업은 대기압 하에서 이루어지는 경우가 많으므로 엔팔피가 열량의 의미를 대체하는 경우가 많습니다.
| 복영근(Pock. young-keun) | www.peaceone.net | dreamer@peaceone.net |
<< 아름다운 문화를 만들어 갑시다 ... ^^ >>