
|
1. 상태함수와 완전미분 (state functions & exact differentials) |
z를 x와 y의 함수로 놓고 전체 미분을 하면 다음과 같이 쓸 수 있습니다.
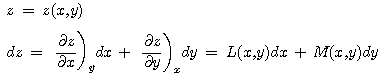
여기서 L(x,y)과 M(x,y)은 각각 z(x,y)를 x와 y로 편미분 한 함수이므로 다음과 같은 관계가 성립함을 쉽게 알 수 있습니다.
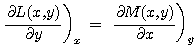
이 관계식을 특별히 Maxwell 관계식(Maxwell relationship)이라고 합니다. Maxwell 관계식이 중요한 이유는 열역학에서 이와 비슷한 형태의 미분방정식이 많이 등장하게 되기 때문입니다.
이 관계를 조금 더 자세히 살펴보기 위하여 L(x,y)과 M(x,y) 대신에 일반화 된 함수 P(x,y)와 Q(x,y)를 정의하고 다음과 같은 미분방정식을 생각해 보도록 하겠습니다.
|
|
|
(1) |
여기서 P(x,y)와 Q(x,y)는 z(x,y)를 x와 y로 편미분 한 함수가 아니며, 독립적인 일반함수입니다. 따라서 모든 z(x,y)에 대해서 Maxwell 관계식이 성립하지는 않습니다. 그러나 어떤 특별한 경우에는 임의의 P(x,y)와 Q(x,y)에 대해서 Maxwell 관계식이 성립하는 경우가 있으며 이를 수식으로 표현하면 다음과 같습니다.
|
|
|
(2) |
즉, 이처럼 식(2)를 만족하는 z(x,y)를 완전하다(exact or perfect)라고 표현하며, 이때의 식(1)을 완전미분방정식(exact differential equation)이라고 부릅니다. 완전미분방정식에서 P(x,y)와 Q(x,y)는 다음의 관계를 만족하며 결국은 L(x,y), M(x,y)과 동일한 의미를 가지게 됩니다.
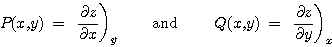
열역학에서는 이처럼 완전미분방정식을 만족하는 함수 z(x,y)는 대단히 중요한 의미를 가지며, 특별히 x와 y의 상태함수(state function)라고 부르고 있습니다. 상태함수의 중요한 특징 중 하나는 다음 그림과 수식에서 보듯이 함수의 변화가 경로에 의지하지 않으며, 변화의 처음과 끝점인 (x1,y1)과 (x2,y2)에만 의존하게 된다는 점입니다.
|
|
|
경로
C에 대한 매개변수 t를 도입하여 상태함수의 중요한 성질인 위 관계를 증명해 보도록
하겠습니다. 그러면 변수 x, y는 각각 t의 함수가 됩니다. 즉, 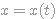 ,
, 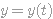 이며 처음과 끝점에 대해서는 다음과 같습니다.
이며 처음과 끝점에 대해서는 다음과 같습니다.
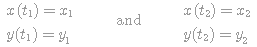
함수 z는 완전미분방정식의 성질을 만족하므로 P(x,y)와 Q(x,y)의 값을 적용하여 적분값을 풀면 다음과 같이 간단히 증명할 수 있습니다.
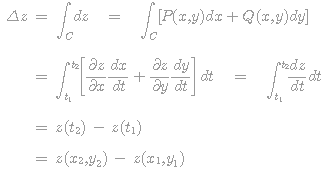
|
2. Chain Rule |
편미분 방정식의 성질 중 하나인 chain rule은 열역학의 일반관계식을 설명하는데 자주 사용되므로 여기서 간단하게 살펴보고자 합니다. 먼저 z를 x와 y의 함수로 가정하는 것으로부터 시작하겠습니다.
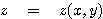
x와 y가 서로 독립적이면 다음과 같이 간단하게 쓸 수 있습니다.
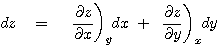
그러나 만일 x와 y가 서로 독립되지 않고 어떤 형태로든지 의존하고 있다면 위 식과는 조금 다른 형태로 표현할 수 있습니다. 예를 들어 변수 y가 x의 변화에 의존한다고 가정하면, z(x,y)는 이 특별한 경로 y=y(x)에 따라 변화하게 됩니다. 즉,
|
|
|
(3) |
|
|
∴
|
(4) |
여기서
함수 z가 고정된 상수라고 가정해 보겠습니다. 즉 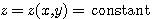 가 되며 이는 고정된 z에 대하여 특별한 경로 y=y(x)를 선택하는 것이 됩니다.
가 되며 이는 고정된 z에 대하여 특별한 경로 y=y(x)를 선택하는 것이 됩니다.
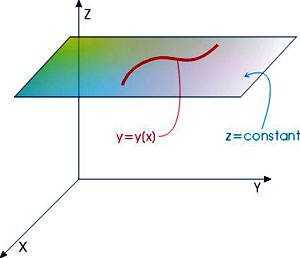
그러면 식(3)에서 dz=0 이 되며 dx는 임의의 변수가 됩니다. 따라서 식(4)로부터 다음의 결과를 얻게 됩니다.
|
|
∴
|
(5) |
같은 방법으로 x=x(y)의 경로를 이용하는 다음의 표현도 같은 형식의 결과를 유도할 수 있습니다.
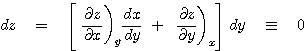
|
|
∴
|
(6) |
식(5)를 식(6)에 대입하면 다음의 식을 얻을 수 있습니다.
|
|
∴
|
(7) |
식(7)이 의미하는
것은 같은 변수를 고정시킨 상태에서는 편미분의 값을 서로 계산할 수 있다는 점입니다.
따라서 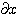 와
와 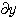 는 서로 약분 가능함을 알 수 있습니다.
는 서로 약분 가능함을 알 수 있습니다.
식(7)을 각각 식(5)와 식(6)에 적용시키면 다음과 같은 매우 유용한 결과를 유도할 수 있습니다.
|
|
∴
|
(8) |
| 복영근(Pock. young-keun) | www.peaceone.net | dreamer@peaceone.net |
<< 아름다운 문화를 만들어 갑시다 ... ^^ >>