경계층이란 어떤 물체의 경계면에 인접한 지역으로서 경계면에 의하여 발생하는 전단 저항때문에 유체의 유속이 변화하는 영역을 지칭한다.  여기서는 수식의 표현을 간단하게 만들기 위하여 시간에 무관한 2차원 공간의 영역을 생각해보고자 한다.  이 경우에서의 연속방정식과 Navier-Stocke방정식은 다음과 같이 표현할 수 있다.

   이 때 경계면의 방향이 x-축이라고 본다면 식(3)은 식(2)에 비하여 무시할 수 있을만 큼 작은 영향을 주며, 결국 다음의 식으로 간단하게 생각해 볼 수 있다.

   여기서 베르누이 방정식을 적용시키면 압력의 항을 변경하여 다음 식을 얻는다.

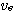는 경계층 외부의 흐름에서의 속도를 의미하며, 일반적으로 유선을 따라 흐르는 포텐셜흐름을 의미한다.

   식(5)에서 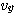를 연속방정식을 사용하면 다음과 같이 변경할 수 있다.

이 식은 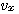를 변수로 가지는 편미분 방정식이 된다.  각 항을 0~∞구간에서 y로 적분하고 정리하면 다음과 같이 표현할 수 있다.  x에 대한 편미분은 y의 적분에 의하여 전미분이 되며, y→∞에서는 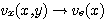로 쓸 수 있다는 것을 참고하도록 한다.

이 식을 정리하고 양 변에 밀도를 곱하면 다음과 같은 결과식을 얻게 된다.

특히 식의 왼쪽 항은 표면에서의 전단응력로 생각할 수 있다.  이 식은 경계층 해의 많은 근사적인 표현을 검사하고 정당화 시키는데 사용되는 경우가 많다.

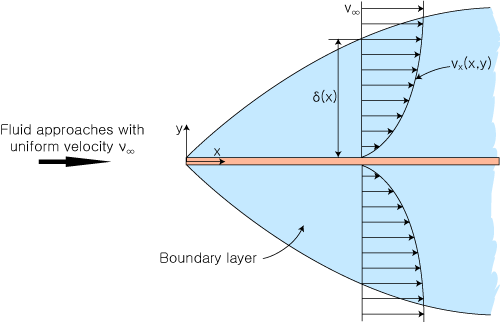
   위 그림은 넓이가 무한한 평판위를 흐르는 층류에 대한 경계층을 표시한 그림이다.  일반적으로 경계층 두께 δ(x)는 자유흐름속도 v_∞의 99%가 되는 지점으로 정의한다.  x=0에서 경계층은 나타나기 시작하고 x가 증가함에 따라 경계층의 두께도 증가하게 되지만 무한히 증가하지는 않는다.

   여기서는 자유속도 v_∞가 시간의 흐름과 x의 증가에 대해서 변하지 않는 상수로 가정할 것이다.  그러면 식(5)는 다음과 같이 간단히 쓸 수 있다.

위 그림을 참고하면 다음과 같은 경계조건이 성립함을 알 수 있다.

   이 문제를 접근하기 위하여 다음과 같은 무차원 수를 도입하여 정리해 보도록 한다.

식(14)의 관계를 식(9)에 적용시키기 위하여 각각의 항을 표현하면 다음과 같이 쓸 수 있다.

식(15)~(19)를 식(9)에 대입하고 정리하면 다음과 같은 미분방정식을 얻을 수 있다.

식(20)에 대응하는 경계조건은 다음과 같이 변경이 된다.

|  복영근(Pock. young-keun)  |  www.peaceone.net  |  dreamer@peaceone.net  |

<< 아름다운 문화를 만들어 갑시다 ... ^^ >>