먼저 아래 그림처럼 무한히 뻗어있는 2차원 벽이 기준시간에서 갑자기 속도 v₀로 움직인다고 가정하면, 유체는 벽의 움직임과 동일한 방향으로 함께 흐르게 될 것이다.  그러나 점성의 영향으로 벽에서 멀어질수록 유체의 속도는 감소하게 되고, 더욱 멀어지면 벽의 움직임에 영향을 받지 않는다.  이러한 성질을 수학적인 도구를 이용하여 표현해보고자 한다.

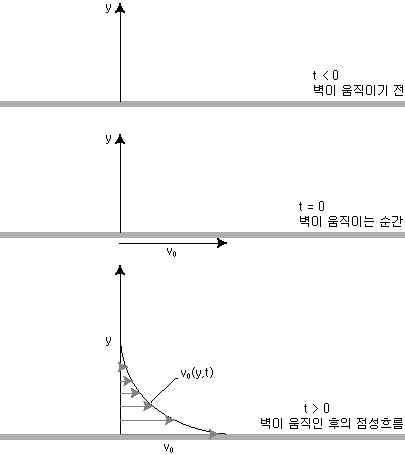
   위 그림을 참고하여 압력변화나 중력의 변화를 무시하면 유체방정식을 다음과 같은 식으로 표현해 볼 수 있다.

여기서 다음과 같은 초기조건과 경계조건이 성립하게 된다.  벽이 움직이는 순간의 시간을 "0"으로 놓으면, 0보다 작은 시간에서는  속도가 없다는 것이 초기조건이 된다.

    속도에 대한 무차원 변수 φ=v_x/v₀를 설정하면 식(1)은 다음과 같이 쓸 수 있다.

식(2)를 더욱 단순화 시키기 위하여 변수통합법(method of combination of varibales)이용하면 다음과 같은 적절한 변수를 설정하여 식에 적용할 수 있다.

식(3)의 설정을 식(2)에 적용하여 다시 쓰면 다음과 같은 식을 얻을 수 있게 된다.

식(4)에 대한 경계조건은 위에 제시한 경계조건을 이용하면 다음과 같음을 알 수 있다.

식(4)를 두 가지 경계조건을 적용하여 풀고 원래의 변수로 되돌려 주면 다음과 같은 결과식을 얻게 된다.

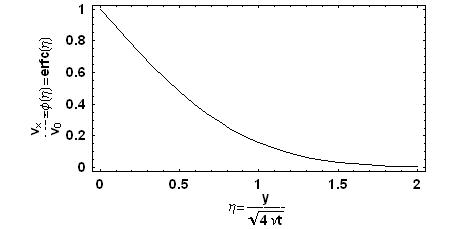
   이처럼 벽이 움직이는 것에 의하여 어느 정도의 거리에 있는 유체는 벽과 함께 흐름을 가지게 되는데, 벽의 움직임의 영향을 받는 정도가 1%가 되는 지점을 일반적으로 경계층 두께(δ)라고 한다.  즉, 벽의 두께가 100이라고 할 때 정지했던 유체의 흐름 속도가 1이 되는 지점을 일컬으며, 위 식과 그래프를 참고하면 다음 식으로 표현될 수 있음을 알 수 있다.

   전달현상론의 특이한 한가지는 세가지 현상에 대하여 물리적인 형태는 전혀 다르지만 수학적인 표현방식은 거의 동일하게 나타난다는 점이다.  이러한 표현은 각 형태의 미분방정식 표현에서도 간접적으로 느낄 수 있지만, 이러한 구체적인 예를 들면 더욱 확실해진다.  위에서 다룬 운동량전달의 표현을 바꾸어서 여기서는 열전달의 예를 들어보고자 한다.

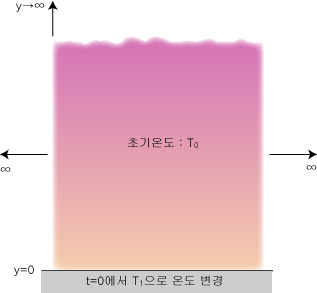
   문제의 상황을 위 그림으로 표현해 보았다.  전체적으로 초기온도 T₀에서 y=0영역에서 갑자기 온도가 T₁으로 바뀌게 된다.  온도가 바뀐 시간을 t=0을 놓으면, 시간이 지남에 따라 열전달에 의하여 온도의 변화가 생기게 된다.  이러한 열전달의 주 방정식은 유체의 흐름이 없고 등압의 경우이므로 미분방정식 표현을 참고하면 다음과 같이 간단하게 표현될 수 있다.

일반적으로 특히 이 경우는 모든 영역의 형태와 물질의 특성이 같으므로 열전달 상수 k는 거리의 함수가 아님을 알 수 있다.  또한 온도의 무차원 변수를 적용시키면 다음과 같이 식(7)을 변형할 수 있다.

이 수학적 표현은 식(2)와 완전히 동일한 경우이다.  따라서 식(8)의 해는 식(5)와 같으며, 무차원 변수를 복원시키면 다음과 같은 결과를 얻게 된다.

여기서 조금 더 나아가, y=0에서의 열 flux는 다음과 같이 계산된다.

즉, 경계면에서의 열 flux는 시간의 제곱근에 반비례함을 알 수 있으며, 직관적으로 예상했던 바이다.

|  복영근(Pock. young-keun)  |  www.peaceone.net  |  dreamer@peaceone.net  |

<< 아름다운 문화를 만들어 갑시다 ... ^^ >>