이동현상은 크게 세가지의 전달현상을 다룬다.  운동량과 열 그리고 물질전달이 이 세가지이다.  이들의 각각 이동현상은 전달매체가 다를 뿐만 아니라 물리적인 이동과정도 매우 상이하다.  그러나 이들의 현상을 설명하는 수학적 체계는 매우 단순하리만큼 일치성을 보이고 있다는 것은 놀라운 점이다.

   여기서 우리가 다루고자 하는 분야는 바로 운동량 전달이다.  이름대로 운동량의 전달현상을 목적으로 하기에 당연히 운동량의 변화를 설명할 수 있는 관계식으로부터 현상을 이해하여야 할 것이다.  이미 앞의 장에서 유체 흐름의 운동량 관계식을 적분형으로 다루어 보았으나, 적분형 식은 여러 현상을 적용하기에 한계가 있기에 이를 더욱 유용한 미분형으로 바꾸어 일반식을 만들어 놓는 것이 여러 가지 이유로 필요할 것이다.

   따라서 이 장에서는 운동량 관계식을 미분형으로 유도하는 과정을 설명하고, 이에 대한 여러 관점을 함께 논하고자 한다.

   유체 운동량의 적분형 관계식을 다음과 같이 유도됨을 전 절에서 다루었다.

   이 관계식을 풀어서 설명하면 다음과 같은 개념관계로 도시할 수 있다.

   이 관계식을 쉽게 설명하기 위하여 식(1)을 대상부피로 나눈 다음 극한값을 취하면 다음과 같이 쓸 수 있다.

이제 이 식을 하나하나의 항으로 분류하여 풀어보도록 하자.

   대상부피에 작용하는 외부 힘의 영향으로는 수직응력과 전단응력, 그리고 중력과 외부로부터 받는 압력의 영향을 적용할 수 있다.  먼저 x 방향으로 작용하는 힘만을 고려한다면 다음과 같이 쓸 수 있다.

식(3)의 형식을 맞추기 위하여 식(4)를 미소부피(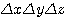)로 나누어 극한을 취하고, 동일한 방법으로 y 방향과 z 방향을 적용하면 다음과 같이 종합할 수 있다.

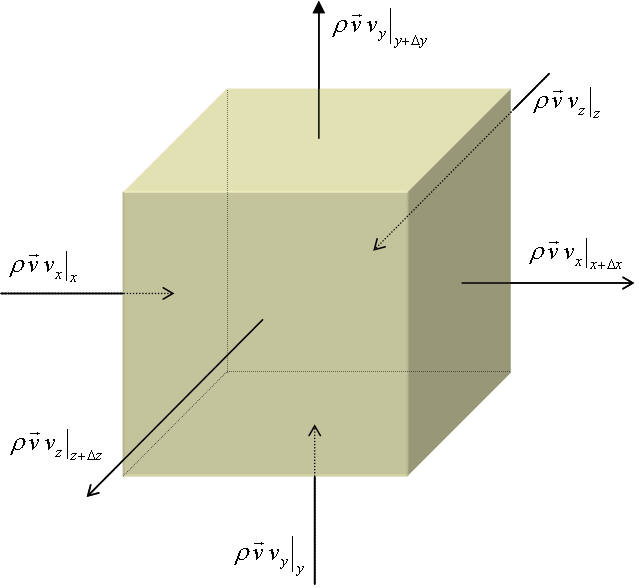
   위 그림은 대상 미소부피를 통과하는 운동량 flux를 표현한 것이다.  이 그림을 참조하여 식(2)와 (3)의 선운동량의 순 유출속도항을 플어서 쓰면 다음과 같이 표현할 수 있다.

마지막 식은 연속방정식을 적용시킨 결과이다.

   지금까지 얻어진 결과들을 종합하면 다음과 같이 정리할 수 있다.

식(8)의 결과식을 식(3)에 대입하고 성분별로 분리하여 쓰면 다음과 같다.

여기서 D/Dt는 전미분을 의미한다.  식(9)는 응력-변형률 관계에 상관없이 모든 유체에 적용할 수 있으며, Stokes의 점도법칙으로부터 다음과 같이 나타낼 수 있다.

이렇게 유도된 식(10)을 Navier-Stokes 방정식이라고 부른다.  물론 이 식은 직교좌표의 경우이다.

   일반적인 경우는 이러한 구속조건을 가지는 경우가 많이 발생한다.  비압축성 흐름의 경우는 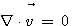이므로, 이 경우에는 다음과 같이 전 좌표의 상황을 하나의 식으로 표현할 수 있다.

   특히 더욱 특수한 경우로서 비점성인 경우 즉, 점도가 '0'인 경우의 식을 Euler의 식이라고 불리며, 다음과 같이 나타낸다.

   Navier-Stokes 방정식을 조금 관점을 달리 하여, 흐르는 유체상에서 에너지 관계성이 어떠한지에 대하여 알아보고자 한다.  식(9)를 벡터형식으로 통합하여 다음과 같이 나타낼 수 있다.

식(13)을 에너지 rate형식으로 나타내기 위하여 양 변에 지역속도를 곱하면 다음과 같이 쓸 수 있다.

식(14)를 각각 의미를 가지는 항으로 풀어서 정리하면 다음처럼 종합할 수 있다.

여기서 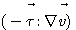항은 Newtonian 흐름에서 항상 (+)값을 가지며, 다음과 같은 의미를 지닌다.

|  복영근(Pock. young-keun)  |  www.peaceone.net  |  dreamer@peaceone.net  |

<< 아름다운 문화를 만들어 갑시다 ... ^^ >>