순수 유체의 기-액 평형을 정의하시 위하여 상태방정식을 이용하는 방법에 대해 논하고자 한다.  우선 평형상태에서 공존하는 상들에 대해서는 다음의 관계식이 성립한다.

Gibbs free energy 평형방정식의 미분형태 및 열역학 관계식은 다음과 같다.

여기서 적절한 상태방정식이 사용 가능하고 이를 이용하여 T와 P의 함수로서 V를 계산할 수 있다고 본다면, 식(3)의 두 번째 관계식만을 고려해 볼 수 있다.  이 식으로 풀어서 정리하면 다음과 같다.

이 유체가 이상기체라면 다음과 같이 표현될 수 있다.

식(4)에서 식(5)를 빼면 다음 관계식을 얻는다.

이 식에서 P1을 0으로 놓고, P=0에서 모든 유체는 이상기체로 간주하면 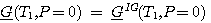이 된다.  따라서 (식)6에서 모든 하첨자를 제거하고 정리하면 다음과 같은 관계를 얻는다.

   여기서 새로운 열역학 함수, 퓨개시티(fugacity)를 문자 f로 정하여 다음과 같이 정의하게 된다.

마지막 항의 φ는 퓨개시티 계수(fugacity coefficient)로 정의된다.

   이같은 정의로부터 퓨개시티는 명백히 압력의 단위를 가지며, P→0으로 접근함에 따라 f→P가 되는데, 이는 고려하는 유체가 압력이 충분히 낮아지면 이상기체상태로 접근하고 퓨개시티는 압력과 같아짐을 뜻한다.  이러한 의미로 볼 때 퓨개시티는 상평형 계산에 유용하게 쓰일 수 있도록 도입된 일종의 대응압력이다.

   식(1)의 의미를 식(8)에 대입하면 정리하면 다음과 같이 표현된다.

이 식을 정리하면 다음과 같은 중요한 상평형 조건을 얻는다.

   퓨개시티의 정의식은 식(8)은 몰부피가 온도와 압력의 함수로 표현되므로 사용하기에 어려운 부분이 많다.  따라서 퓨개시티와 부피에 대한 적분식을 관련시키는 것이 더욱 편리할 수 있다.  이러한 표현으로 다음과 같이 나타내었다.

여기서 Z=PV/RT는 압축인자이다.

*  이상기체의 경우

*  비리얼 상태방정식

여기서 Z는

* van der Waals 상태방정식

*  Peng-Robinson 상태방정식

* 비압축성을 고려한 액체의 퓨개시티

*  순수고체의 퓨개시티

|  복영근(Pock. young-keun)  |  www.peaceone.net  |  dreamer@peaceone.net  |

<< 아름다운 문화를 만들어 갑시다 ... ^^ >>