
|
System의 평형상태에 관한 모든 열역학적 정보를 포함하고 있는 방정식 |
|
1. 에너지 표현 (energy representation) |
에너지 U는 상태함수이므로, 어느 평형상태에서 다른 평형상태로의 변화량 ΔU는 가역과정으로 가정하고 계산할 수 있습니다. 따라서 설정한 시스템이 평형상태로 향하는 과정을 표현하는 방정식은 다음과 같이 쓸 수 있습니다.
|
|
|
(1) |
식(1)은 바로 열역학적 기본방정식의 에너지에 대한 표현이며, 여기서 에너지 함수 U는 엔트로피(S)와 부피(V)의 함수로 표현할 수 있기 때문에 각각 S와 V에 대한 편미분방정식 형식으로 표현할 수 있습니다.
|
|
|
(2) |
식(1)과 식(2)를 비교하면 기본방정식으로 유도되는 매우 유용한 관계식을 얻을 수 있습니다. 이렇게 얻어진 방정식을 멕스웰 관계식이라고도 부릅니다.
|
|
|
(3) |
|
|
|
(4) |
다른 과점으로 식(1)을 변형하여 엔트로피의 표현인 다음 식(5)의 형식으로 표현할 수 있고, 이것 또한 열역학적 기본방정식으로 엔트로피 표현입니다.
|
|
|
(5) |
에너지표현에서와 같은 형식으로 식(5)를 이용하여 다른 모양의 멕스웰 방정식을 얻을 수 있습니다.
|
|
|
(6) |
|
|
|
(7) |
지금까지 과정에서 얻어진 열역학적 기본 방정식은 에너지와 엔트로피의 형식을 이용하여 평형상태를 설명하는 완벽한 방정식입니다. 그러나 식(1)을 이용하여 평형상태를 설명하기 위해서는 온도(T)와 엔트로피(S)의 변화를 측정해야만 합니다. 마찬가지로 식(5)를 이용하기 위해서는 에너지(U)와 부피(V)를 측정하는 과정이 필요합니다. 온도와 부피는 실제 세계에서 측정하기가 쉬운 것에 반하여 엔트로피와 에너지의 변화를 측정한다는 것은 매우 어렵습니다. 따라서 기본 방정식의 평형특성에 대한 정보를 손실하지 않으면서 측정하기 쉬운 압력(P), 온도(T), 부피(V)등의 양으로 표현할 수 있다면 매우 실제 현상에 적용하기에 적합한 표현이 될 수 있을 것입니다. 이러한 이유로 식(1)과 식(5)를 르장드르 변환법칙(Legendre transformation)을 이용하여 P, T, V 세 개의 상태량으로 표현되는 상태함수를 정의할 수 있습니다. 이러한 상태함수를 정의하기 전에 르장드르 변환에 대해서 간단히 알아보겠습니다.
|
2. 르장드르 변환 (Legendre transformation) |
르장드르 변환이란 임의의 함수 y=y(x)를 기울기(p)와 y 절편(ψ)으로 표현하는 과정을 의미합니다. 어느 함수의 임의의 점에서 결정되는 기울기와 y 절편은 독립된 값을 가지게 되지만, x와 y의 변화에 대응하는 변수의 형태로 나타낸다면 다음처럼 표현될 수 있습니다.
|
|
|
(8) |
예를 들어 y=x2/4를 르장드르 변환을 하면 다음과 같이 됩니다. 임의의 점에서의 기울기 p는 x/2 이므로, y=p2 이 된다. 따라서
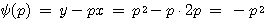
|
3. 기본 방정식의 다른 표현들 |
르장드르 변환을 이용하여 대표적인 기본방정식들을 표현한 것이 다음과 같습니다. 물론 다른 표현들도 가능하겠지만 이러한 표현법이 가장 많이 사용되고 있습니다. 여기서는 닫힌계(close system)에 대한 표현들이며, 열린계(open system)에 대한 표현은 나중에 살펴 볼 수 있을겁니다.
|
내부에너지(U) |
|
dU = TdS - PdV |
|
Enthalpy(H) |
H = U + PV |
dH = TdS + VdP |
|
Helmholtz free energy(A) |
A = U - TS |
dA = -SdT - PdV |
|
Gibbs free energy(G) |
G = H - TS |
dG = -SdT + VdP |
| 복영근(Pock. young-keun) | www.peaceone.net | dreamer@peaceone.net |
<< 아름다운 문화를 만들어 갑시다 ... ^^ >>