
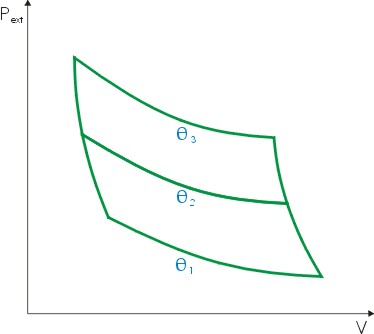
이 그림은 세 개의 실험온도 θ1, θ2, θ3에서 작동되는 서로 상이하게 해석할 수 있는 세 개의 카르노 사이클을 표시한 것입니다. 먼저 θ1과 θ3에서 작동하는 카르노 사이클 효율은 다음과 같습니다.
|
|
|
(1) |
같은 방법으로 나머지 두 개의 카르노 사이클 효율을 표현할 수 있습니다.
|
|
|
(2) |
|
|
|
(3) |
이 식을 좀 더 다루기 쉬운 표현으로 바꾸기 위하여 다음처럼 표현해 보았습니다. 여기서 함수 g는 양의 값을 갖는 함수입니다.
|
|
|
(1') |
|
|
|
(2') |
|
|
|
(3') |
이들 세 개의 함수 g의 관계를 연결하여 보면 다음의 관계가 성립함을 알 수 있다.
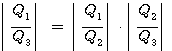
|
|
|
(4) |
θ1과 θ3 사이에서 존재하는 θ2가 임의의 모든 값에서 식 (4)를 만족하기 위해서는 함수 g의 형태가 다음과 같이 표현되어야 합니다.
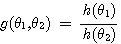
함수 g가 이런 형태가
되지 않으면 식(4)의 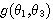 는 θ2의 영향을 받게 될 것이기 때문입니다. 이러한 함수 g의
형태를 식(1'), (2'), (3')에 대입하여 열량 Q의 표현을 유도하면 다음과 같은 결과를
얻을 수 있습니다.
는 θ2의 영향을 받게 될 것이기 때문입니다. 이러한 함수 g의
형태를 식(1'), (2'), (3')에 대입하여 열량 Q의 표현을 유도하면 다음과 같은 결과를
얻을 수 있습니다.
|
|
|
(5) |
식(5)에 등장하는 T1과 T3를 열역학적 온도(thermodynamic temperature scale)라고 정의합니다. 이처럼 열역학적 온도는 카르노 사이클을 통하여 직접 얻을 수 있습니다. 카르노 사이클의 효율을 열역학적 온도를 사용하여 표현하면 다음 식(6)과 같습니다.
|
|
|
(6) |
여기서 카르노 엔진 효율이 1이 되는 저온 저장소의 온도를 열역학적 온도 T가 "0"인 온도로 정의합니다. 바꾸어 표현하면 카르노 엔진의 효율은 저온 저장소의 온도가 0K일 때 1이 됩니다.
|
이상기체에서의 온도 정의(ideal gas temperature scale) |
이상기체의 온도스케일은 다음의 상태함수로 정의됩니다.
|
|
|
(7) |
식 (7)의 정당성은 카르노 사이클에 적용함으로서 증명할 수 있습니다. 열팽창 계수를 사용하여 식 (7)을 적용시키면 다음과 같이 됩니다.
|
|
|
(8) |
이 관계를 수치적으로 표현하기 위하여 식(7)을 그래프로 표현해 보면 다음과 같습니다.
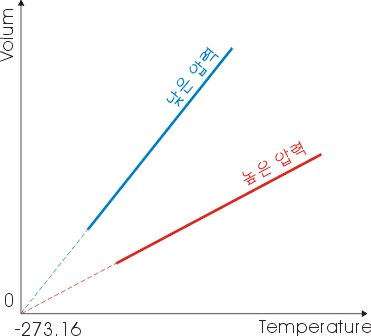
즉, 임의의 압력에서 이상기체의 부피는 -273.16℃에서 0이 됨을 알 수 있습니다. 이러한 가장 최하한의 온도를 열역학적 기준온도로 표현하여 절대온도 0K로 정의하며, 섭씨 온도와는 다음의 관계를 유지합니다.
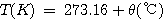
| 복영근(Pock. young-keun) | www.peaceone.net | dreamer@peaceone.net |
<< 아름다운 문화를 만들어 갑시다 ... ^^ >>