
질량 m의 입자가 일정한 총 에너지 E를 가지고 (+)방향으로 입사되는 과정을 생각해 보도록 한다.
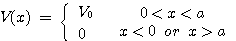

위 관계를 해석하기 위해서 시간에 무관한 1차원 Schrodinger 방정식을 다음과 같이 도입하도록 하자.
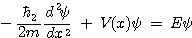
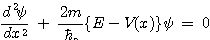
이 방정식을 풀어서 각 영역에 해당하는 형태를 고려하면 다음과 같이 종합적으로 표현할 수 있다.

여기서
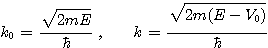
해석을 쉽게 하기 위해서 입사파의 계수는 1로 했으며, 반사계수는 R 그리고 투과계수는 T로 놓았다. 미지의 상수 R, C, D, T를 얻기 위해서 각각의 경계조건을 대입시키면 다음과 같은 네 개의 식으로 이루어진 연립방정식을 얻고, 이를 풀어서 각각의 값을 구할 수 있다.
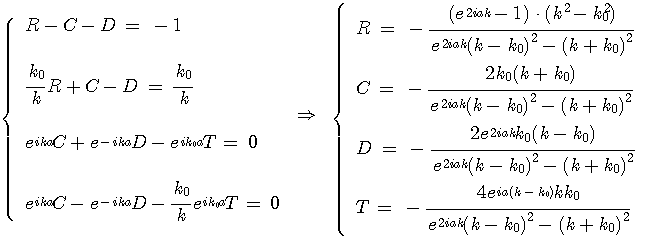
여기서 중요한 것은 입사파수와 투과파수이다. 이 두 파수를 삼각함수를 이용하여 표현하면 다음과 같다.
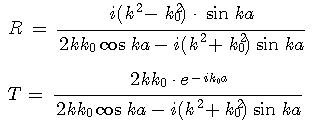
▒▒▒ E < V0 인 경우 ▒▒▒
이 경우에 파수 k는 허수가 된다. 따라서 다음과 같이 실수 q를 도입하여 표현하는 것이 도움이 된다.
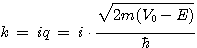
이렇게 도입한 새로운 파수 q를 적용하여 각 영역에서의 파동함수를 변경하면 다음과 같이 된다.
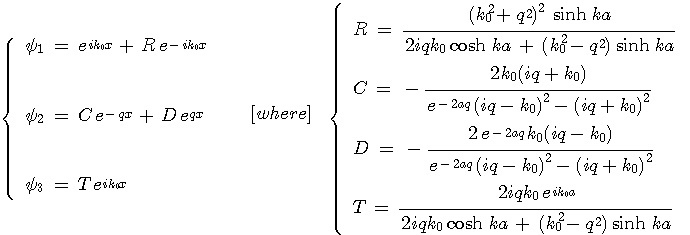
이렇게 얻은 파동함수를 이용하여 가가 영역에서의 확률밀도를 계산하여 보면 다음과 같은 그래프를 얻을 수 있다.
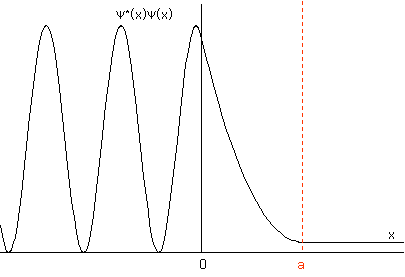
x>a인 영역(3)에서 파동함수는 정상파의 형태를 가지므로 확률밀도는 일정한 값으로 유지되게 된다. x<0인 영역(1)에서도 역시 정상파의 형태를 가지지만 x=0에서 반사된 파의 영향으로 그림과 같이 확률밀도는 진동을 하게 된다. 그림에서는 잘 나타나지 않지만 반사파의 영향으로 밀도의 극소값은 0보다 조금 큰 값을 가지게 된다. 0<x<a인 영역(2)에서는 두가지 형태의 성분을 모두 가지는 복잡한 형태가 되지만 주로 지수함수에 영향을 크게 받는 감소하는 진폭을 가지는 파형이 된다.
그림에서 보는 바와 같이 장벽 포텐셜에 부딪히는 입자는 전부 반사되는 것이 아니고 일부는 장벽을 통과(?)하여 유유히 장벽 반대편에서도 존재할 수 있는 확률을 가지게 된다. 이러한 현상은 거시역학에서는 이해할 수 없는 매우 특이한 현상으로 터널효과라고 부르기도 한다. 터널효과를 더 자세히 보기 위하여 투과계수(t)를 구해보도록 하자. 투과계수 t는 입사파의 흐름에 대한 투과파의 흐름의 비로 구할 수 있다. 즉,
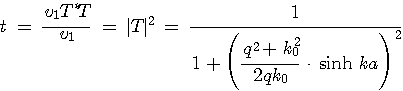
이 때 V0가 매우 클 경우는 다음과 같이 근사식으로 해석할 수 있다.
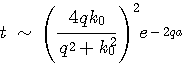
이 식에서 중요하게 작용하는 항은 감소하는 지수항이 된다.
| 복영근(Pock. young-keun) | www.peaceone.net | dreamer@peaceone.net |
<< 아름다운 문화를 만들어 갑시다 ... ^^ >>