
|
시간에 무관한 3차원 Schrodinger 방정식과 세부 방정식 |
시간에 무관한 3차원 Schrodinger 방정식은 직교좌표보다는 구면 극좌표를 사용하는 것이 해석을 하는데 있어서 더 많은 도움이 된다. 구면 극좌표계에 대한 방정식의 표현은 다음과 같이 간단하게 확장하여 표현할 수 있다. 여기서 질량은 환산질량으로 표현하는 것이 정확하기에 m 대신에 μ로 표기하기로 한다.
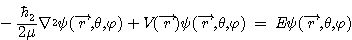
↓
|
|
양자역학에서의 각운동량 연산자는 다음과 같은 중요한 성질을 갖는다.
즉, 세가지 인자 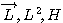 는 서로 교환 가능함을 의미하고, 따라서 H의 고유함수는 동시에
는 서로 교환 가능함을 의미하고, 따라서 H의 고유함수는 동시에 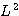 의 고유함수가 되도록 선택할 수 있다. 이러한 기교를 사용하면 H의 고유함수를
구할 때에 간단한 몇몇 함수들의 결합으로 나타낼 수 있기 때문에 매우 강력한 해석적
도구를 제공받을 수 있게 된다. 이와 같은 성질을 이용하면 파동함수
의 고유함수가 되도록 선택할 수 있다. 이러한 기교를 사용하면 H의 고유함수를
구할 때에 간단한 몇몇 함수들의 결합으로 나타낼 수 있기 때문에 매우 강력한 해석적
도구를 제공받을 수 있게 된다. 이와 같은 성질을 이용하면 파동함수 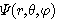 의 해석을 각각의 변수에 관련된 함수의 곱으로 표현할 수 있고 결과적으로 다음과
같은 형식을 취하게 된다.
의 해석을 각각의 변수에 관련된 함수의 곱으로 표현할 수 있고 결과적으로 다음과
같은 형식을 취하게 된다.
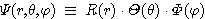
여기서 각각의 함수를 만족하는 방정식은 다음과 같다.
|
|
|
이 함수의 풀이는
각좌표에 관련된 함수 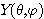 와 길이에 관련된 함수
와 길이에 관련된 함수 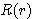 구분하여 해석하는 것이 일반적이며 수소원자와 같은 1전자원자의 경우 다음과
같이 구할 수 있다. 여기서 특히
구분하여 해석하는 것이 일반적이며 수소원자와 같은 1전자원자의 경우 다음과
같이 구할 수 있다. 여기서 특히 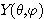 를 구면조화함수라고 부르며 여러 분야에서 자주 등장하게 된다. 또한
를 구면조화함수라고 부르며 여러 분야에서 자주 등장하게 된다. 또한
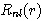 를 흔히 원자의 지름방정식이라고 부르기도 한다.
를 흔히 원자의 지름방정식이라고 부르기도 한다.
|
|
|
|
**
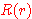 의 방정식
의 방정식
먼저
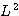 의 고유치 문제의 해를
의 고유치 문제의 해를 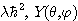 라고 하면
라고 하면
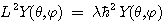
가 된다. 이때
H의 고유함수 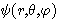 가
가 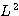 의 고유함수가 되도록 하기 위해서는
의 고유함수가 되도록 하기 위해서는 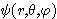 가
가 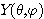 의 인자인
의 인자인 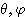 에 무관한 값을 곱하는 형태인 다음과 같은 표현을 선택해야 한다.
에 무관한 값을 곱하는 형태인 다음과 같은 표현을 선택해야 한다.
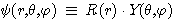
이 관계를 파동방정식에
대입하여 정리하면 다음과 같은 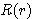 의 식을 구할 수 있다.
의 식을 구할 수 있다.
|
|
**
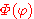 의 방정식
의 방정식
같은
방법으로 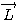 과
과 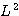 도 교환 가능하므로
도 교환 가능하므로 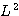 의 고유함수
의 고유함수 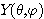 가 동시에
가 동시에 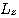 의 고유함수가 되도록 선택할 수 있다.
의 고유함수가 되도록 선택할 수 있다. 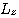 의 고유치를 a, 고유함수를
의 고유치를 a, 고유함수를 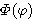 라고 한다면 다음과 같이 표현할 수 있다.
라고 한다면 다음과 같이 표현할 수 있다.
|
|
|
** 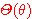 의 방정식
의 방정식
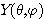 가
가 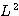 과
과 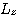 의 공통된 고유함수가 되려면
의 공통된 고유함수가 되려면 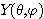 는
는 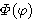 의 인자인
의 인자인 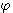 에 무관한 함수를 곱하는 형태를 취해야 한다.
에 무관한 함수를 곱하는 형태를 취해야 한다.
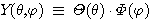
이 관계를 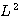 의 고유치 함수에 적용시키면 다음과 같은 방정식을 얻을 수 있다.
의 고유치 함수에 적용시키면 다음과 같은 방정식을 얻을 수 있다.
|
|
| 복영근(Pock. young-keun) | www.peaceone.net | dreamer@peaceone.net |
<< 아름다운 문화를 만들어 갑시다 ... ^^ >>